为我院2022级数学与应用数学专业的同学带来主题《HPM视角下的数学教学——从勾股定理的历史、证明、推广谈教学》的线下讲座。本次讲座由理学院陈振华老师主持。

一、专家简介
杨孝斌,男,汉族,博士、教授、硕士研究生导师,贵州师范大学数学教育研究所所长,贵州师范大学小学数学教学质量强基行动指导中心主任,中国少数民族教育学会数学教育专业委员会常务理事,中国数学会数学教育分会数学教育与数学文化工作组成员,贵州省民族地区基础教育质量指导委员会数学学科指导专家组成员。主要从事数学教育、民族数学文化、HPM(数学史与数学教育)等的研究。主持获得贵州省第五届中小学(幼儿园)优秀教学成果一等奖等四项省级奖项、参与获得2014年国家级教学成果(基础教育类)二等奖。

二、主持人

三、内容提要
(一)数学史在数学教育中的意义和作用






杨孝斌教授对数学史的意义进行综合总结,学习数学史可以帮助人们——产生对数学的强烈兴趣,理解数学的本质,形成正确的数学观,掌握数学的思想与方法,重走数学家数学发现的(思维的)关键性步子。
(二)开展教育取向的数学史研究
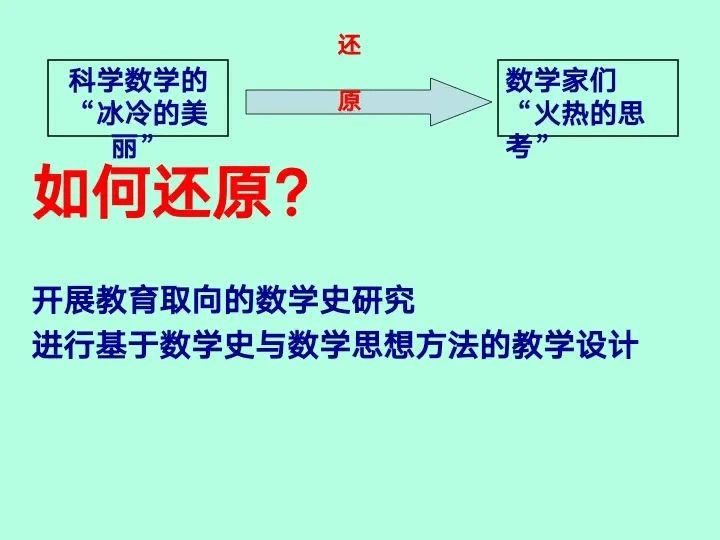
杨孝斌教授提出三个问题,一是数学史要学习什么?二是教科书往往用一种“冰冷的美丽”将数学知识呈现出来,如何将这种冰冷的美丽还原为数学家的“火热思考”?三是何为“教育取向的数学是研究”?围绕这三个问题开展教育取向的数学史研究。所谓教育取向的数学史研究,就是从课程与教学的角度出发,对数学史的相关内容进行教学法加工和方法论重建,以实现科学数学的教学化,达成数学史研究的教育目的。其主要方法是通过对数学史的压缩、整合、册繁就简、提炼数学思想方法等,并在此基础上结合教学内容进行基于数学史和数学思想方法的教学设计。


(三)勾股定理的历史
杨孝斌教授提到在很早以前,许多民族都对勾股定理进行过研究。在古代巴比伦、古代中国、古埃及、古希腊等文明中,都有关于勾股定理的研究。对于古巴比伦文明,最近两个世纪以来发现了无数那个古老文明留下的文物----泥板。在众多的泥板中有一块编号为普林顿322号收藏品有对勾股定理的运用。在西方,勾股定理被称之为“毕达哥拉斯定理”。相传2500年前,有一次毕达哥拉斯在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种特性。同样地,在我国古代很早就有了对勾股定理的研究。在我国的《周髀算经》一书中已经有了关于勾股定理的记载。


(四)勾股定理的证明
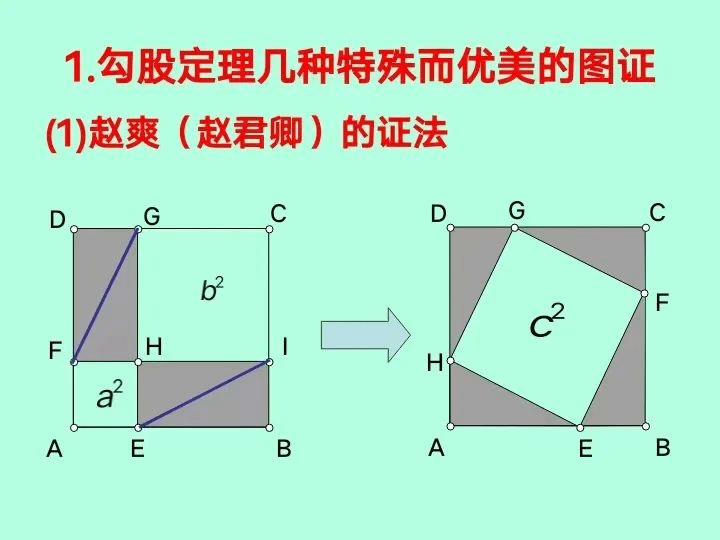
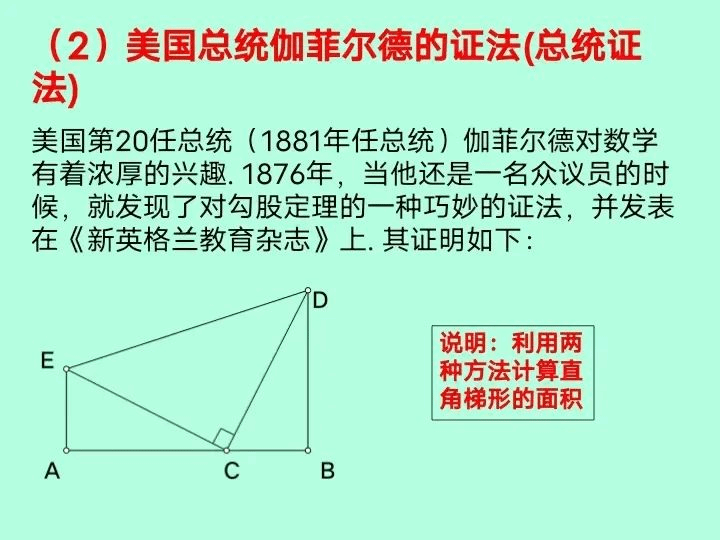
勾股定理提出距今虽已有三千余年,但各种证明方法至今仍接连涌现。据不完全统计,现在世界上已找到了勾股定理的证明方法400余种。由鲁密斯(Loomis,又译作卢米斯)搜集整理的《毕达哥拉斯》(1940年前后)一书就给出了370种不同的证法。
(五)勾股定理的推广
杨孝斌教授从边上图形的一般化、边上图形不相似、推广为任意三角形、推广为凸多边形、空间中的类比定理、从勾股定理到费马大定理等方面讲述勾股定理的推广。欧几里得在《几何原本》中记述了勾股定理的一个推广,即“直角三角形斜边上的一个多边形,其面积等于两直角边上两个与它相似的多边形面积之和。”


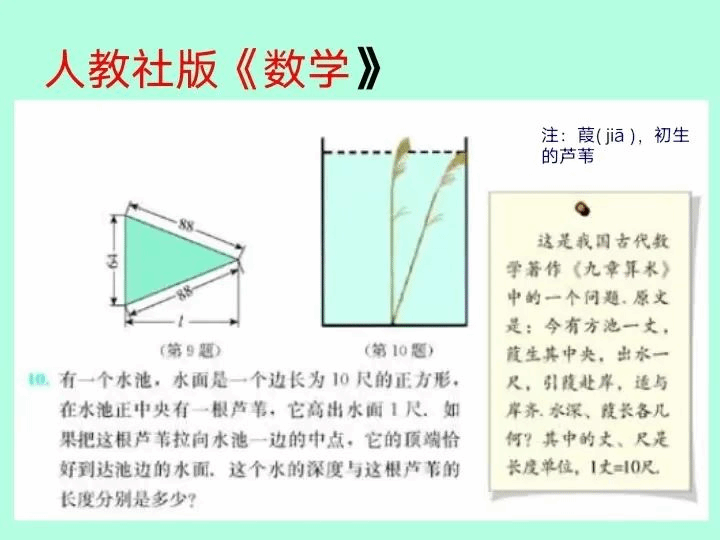
(六)教材中的勾股定理的古算题
杨孝斌教授对华师大版《数学》、人教社版《数学》、北师大版《数学》中对教材中的勾股定理的古运算进行展示。


在讲座中,同学们积极向上、认真听讲。杨孝斌教授针对知识点与同学们互动,同学们认真听讲并发表自己的见解,并且同学们对讲座中出现重要的知识点进行详细的记录。




杨孝斌教授的《HPM视角下的数学教学——从勾股定理的历史、证明、推广谈教学》讲座在同学们热烈的掌声中圆满结束,同学们在这场讲座中收获颇多,不仅打破了同学们以往思考问题的方式,而且让同学们意识到发散思维的优点。相信本次讲座对同学们的数学与应用数学的专业成长有很大的帮助。
